Art, Math, Music: Connected~ Who knew!? This guy.
Turns out this Benno Moiseiwitsch guy was pretty amazing.
This is his explication on why art, math, and music are all actually the same thing. Very interesting stuff.
The Harrow And The Harvest
If you haven’t heard of the musical duo that is Gillian Welch and David Rawlings, consider this your lucky day. You’re going to love this group.
Gillian was one of the “sirens” in the 2000 Odyssey remake by the Coen brothers, O Brother, Where Art Thou, along with Alison Krauss. The producer on that record is the great TBone Burnett.
David Rawlings and Gillian Welch met at Berklee College of Music, apparently. My alma mater! 😛
They’re part of a folk music revival that has been picking up steam for a long time, but that has been reaching a fevered pitch in the last five years or so.
If you’re just getting into Gillian Welch, I’d suggest starting with the album Revival. My favorite song on it is “One More Dollar.” It’s the story of a boy who leaves the mountains to work in the fruit orchards out West, but when there’s a freeze on the branches he’s compelled to risk his savings by gambling in order to afford passage home. He works for a dime a day, and he only needs one more dollar to go home. So the song is sad, but there’s a hopeful energy that comes from the anticipation of making that last dollar.
Time (The Revelator) is also quite good. There are many “whistlers” and “toe-tappers” on that album.
However, there is one song in particular that has really caught my attention off the new record The Harrow And The Harvest. The song is called “The Way It Will Be.”
The music matches the lyrics well in this song. The tone I come away with from both is that of melancholic resignation, with a little bite of anger underneath.
The opening verse exemplifies perfectly this sentiment.
“I lost you awhile ago
But still I don’t know why
I can’t say your name
Without a crow flying by”
Just that is magical. I know exactly that feeling.
And then…
“Gotta watch my back now
That you turned me around
Got me walking backwards
Into my hometown”
<Reading Rainbow segue melody>
Welp, I really enjoyed this album for its close and tight harmonies, its lugubriousness, and its verisimilitude.
Butcha don’t have to take my word for it!
New Note:
I’m gonna see Gillian Welch and David Rawlings at ACL 2011 this weekend. I’ll definitely be updating this post with further details.
A Brief History of Infinity – A Paradox
A good little read. This book taught me a lot of things about set theory and Georg Cantor. It also taught me about a very interesting paradox within set theory, that was identified by Bertrand Russell.
It goes something like this.
Set theory is something so simple that we take it for granted. It merely points out that certain things, although not identical to one another, are similar enough to be grouped into a “set.”
In fact, set theory is where the working concept of numbers in general finds canon. For instance, the number one looks like this in set theory:
{{Ø}1}
The symbol we as a people have for the concept of the number one (1) is a “set,” which is contained by brackets.
The “Ø” is called the empty set.
Brackets contain the emptiness of the empty set, and it is denoted by {}. The empty set being “Ø,” and Ø being equal to zero for most intents and purposes.
{} = Ø
The number two in set theory could be written like this:
{{{Ø}1}2}
The number two contains the number one, which contains the empty set. The pattern here is that the number three would contain the number two, which contains the number two, which contains the number one, and so on. This can be repeated to infinity, in nested brackets form. Cantor considered numbers this way. And came up with the whole idea of transfinite numbers, which are numbers beyond infinity. The book above goes over this concept quite nicely.
Now that we have some contextual knowledge of set theory, the foundation of all mathematics. Here’s what’s wrong with it!
Consider the set of all <somethings>. <somethings> could be anything you want.
Let’s say “llamas,” the set of all llamas.
I denote this set, the set of all llamas, in red for easier reference. Trust me, this gets kinda twisted.
So please consider the set of all llamas. Now the fact that there is a set of all llamas implies that there is an inverse set, a set of all NOT llamas which shall henceforth be denoted in green. Now lots of things fall into the set of all NOT llamas category: you, me, a planet, electrons, horses, etc. Anything that isn’t a llama falls into this category. You’re not a llama. I’m not a llama. Planets aren’t llamas, and vice versa, even though a llama might exist on a planet. And the same goes for electrons. There are obviously a lot of electrons that might be considered “in” or “part of” a llama, but a llama is definitely NOT an electron and vice versa. The same goes for the set itself.
The what?
The set itself. The container. The thing that we named “set of all llamas.”
A set is a concept, it’s a thought. Isn’t that a thing?
But wait, thoughts and feelings are ephemeral. They’re not real things.
Are then none of your thoughts real things that can be considered part of a set? And how do these non-things keep making and changing real things? I mean, if you want to get technical about it, thoughts are a bio-chemical reaction and that’s definitely about as physical and real as anything.
So anyway,
Please consider the fact that the set of all NOT llamas is a member of itself?
A member?
Yes, an element, a constituent, a part of the whole. The set itself is not a llama, and so that set is a member of itself.
So let’s generalize, and consolidate, what knowledge we’ve gleaned.
There are at least two types of sets. There are sets that ARE members of themselves, and sets that are NOT members of themselves. For instance, the set of all llamas is not a member of itself, but the set of all NOT llamas is a member of itself. And this general rule applies to all sets. That’s why we chose “llamas,” arbitrarily.
So let’s just consider the sets that are NOT members of themselves, for a second. We’ll call this super set the set of all sets that are NOT members of themselves.
Now let’s ask ourselves the same question we asked about the other sets to categorize them. Is this set a member of itself, or not?
Let’s explore both possibilities.
The set of all sets that are NOT members of themselves IS a member of itself.
– Well then it’s actually not a member of itself by definition. If it’s a member of the set of all sets that are NOT members of themselves, then it can’t be a member of itself…if it is a member of itself.
The set of all sets that are NOT members of themselves IS NOT a member of itself.
– Paradoxically, it IS a member of itself since it’s NOT a member of itself.
Bertrand Russell pointed out this paradox within set theory, and proved it mathematically.
He doesn’t propose a new theory of “the way things work,” but merely points out that set theory albeit useful might not be the way things actually work.
Someday my “prints” will come…
Someday my prints will come – 60 sec spot for Walmart One Hour Photo
A silly project, along the lines of the Bud Light Beer Ball commercial spot, I did in college for Walmart One Hour Photo. A bit tongue in cheek version of “Someday My Prince Will Come” from the 1937 Disney movie “Snow White.”
College Marketing
01-1 feel like drinkin bud 60 sec
In college, I was assigned the project of creating a 2 spots for a commercial, the product of which we could choose. My friends and collaborators had the good idea of marketing to the Bud Light Beer Ball with the song “Feel Like Makin’ Love” by Bad Company. And yes, there really is/was a Bud Light Beer Ball. See exhibit A.
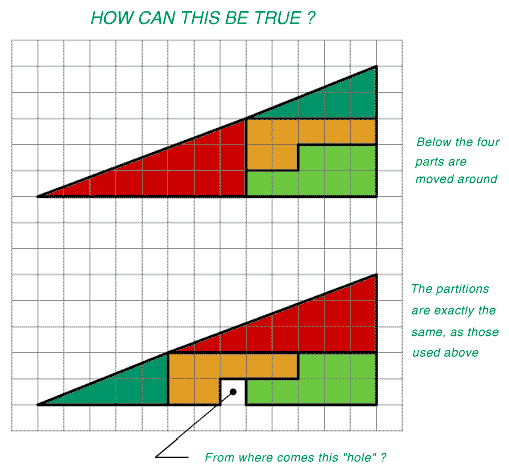
Triangle Paradox
My friend Shi introduced me to this problem. When the answer dawns on your understanding, you feel ridiculous.
Say “maths” not “math.”
If you want to sound like you know what you’re talking about, apparently you have to say “maths” instead of “math.”
Go figure. Tell me what you get.
Guitar Chord Dictionary
I was so sick in this picture. Literally…ill.
At this link you’ll find the remains of a Guitar Chord Dictionary I created with Ryan Vaughn, for ExpertVillage.com. Expert Village was started by the dude who created MySpace.com. He sold his company to Rupert Murdoch, News Corp, and started Expert Village. I believe he ended up selling Expert Village to eHow.com. These videos went everywhere as a result. There were something like 5000 one minute videos, that illustrated all manner of chords on each set of strings. I never went over spread voicings though.
The above video is an instructional video on how to play part of a Wes Montgomery solo. The solo in question is from the D Natural Blues.