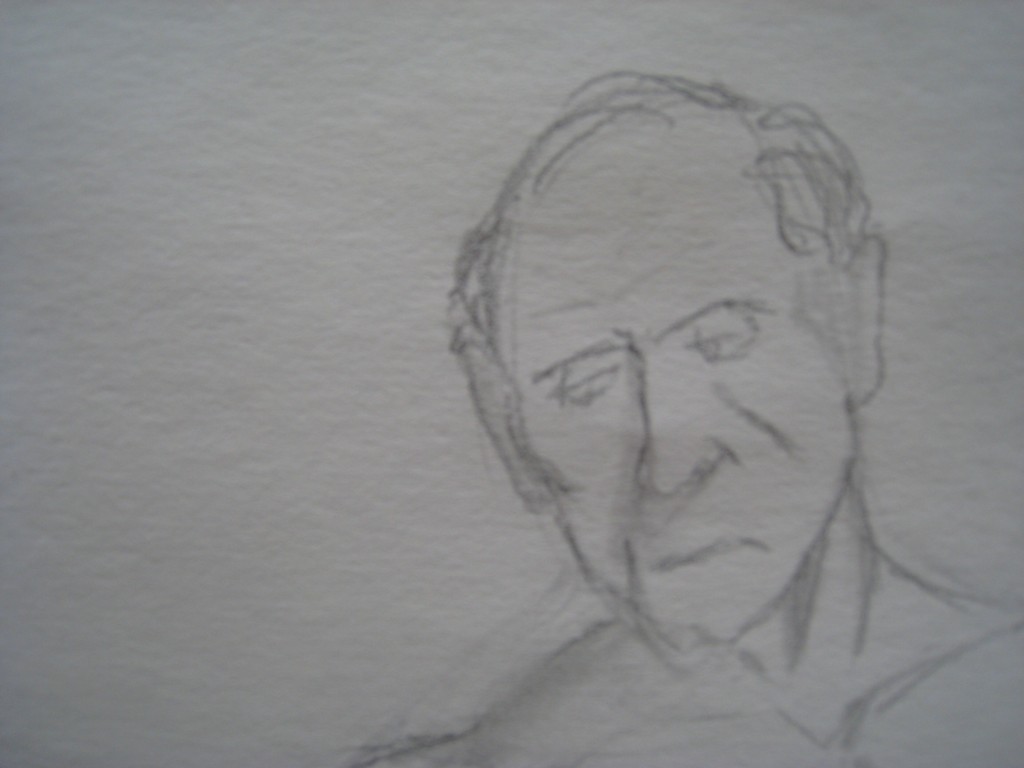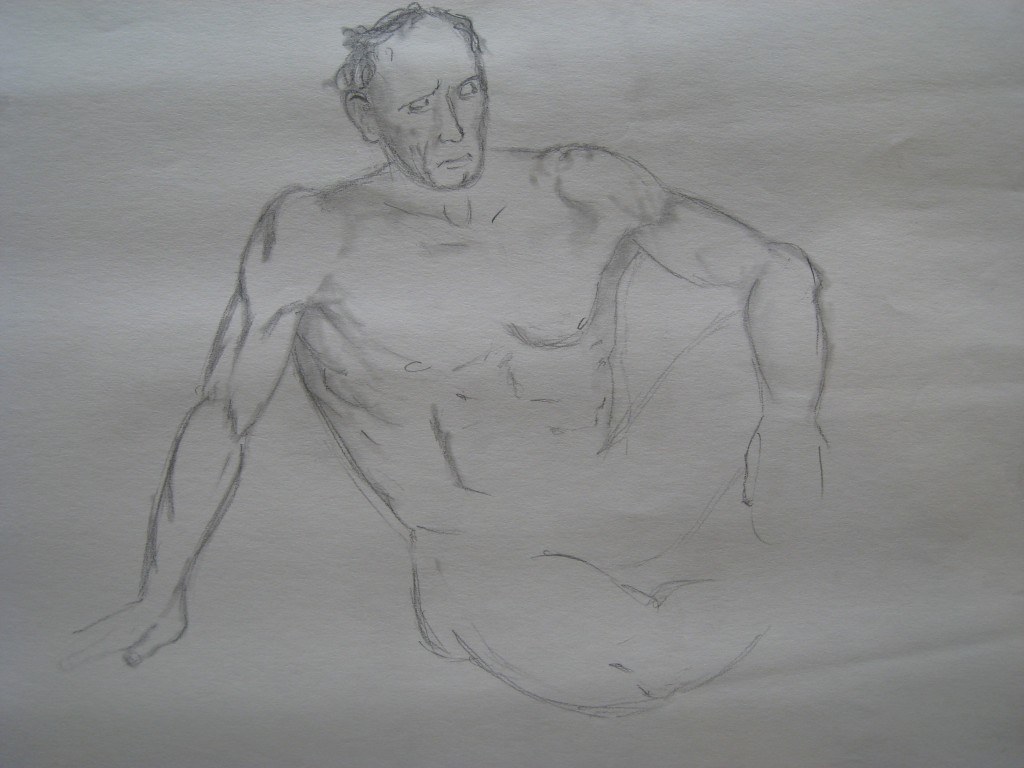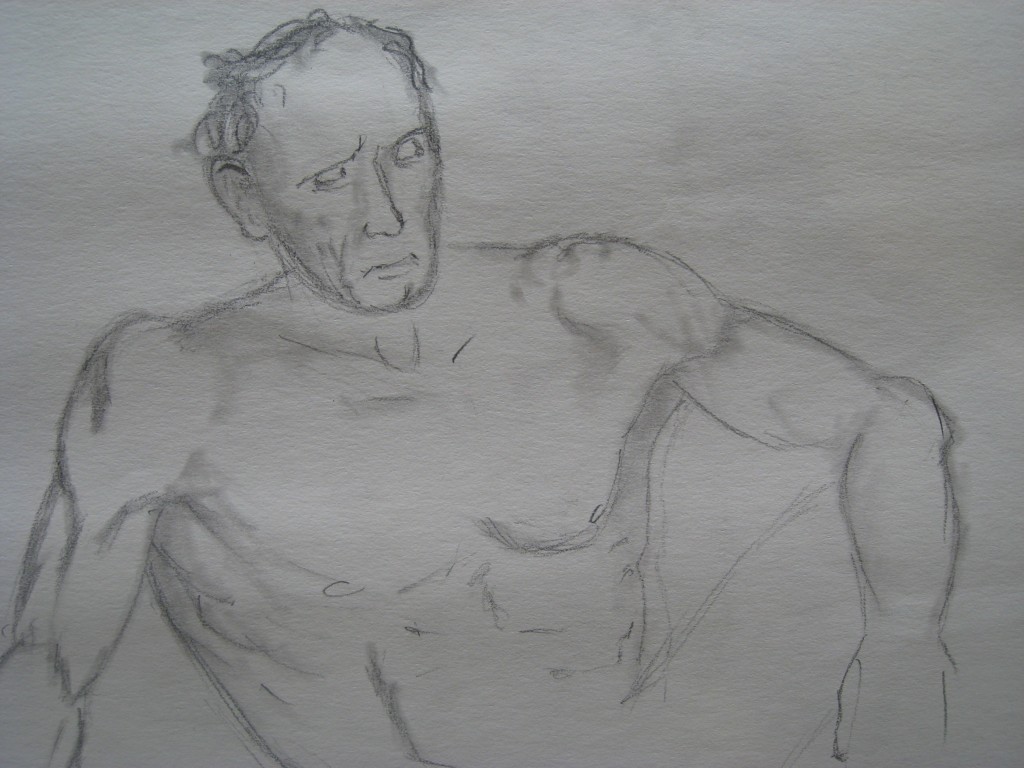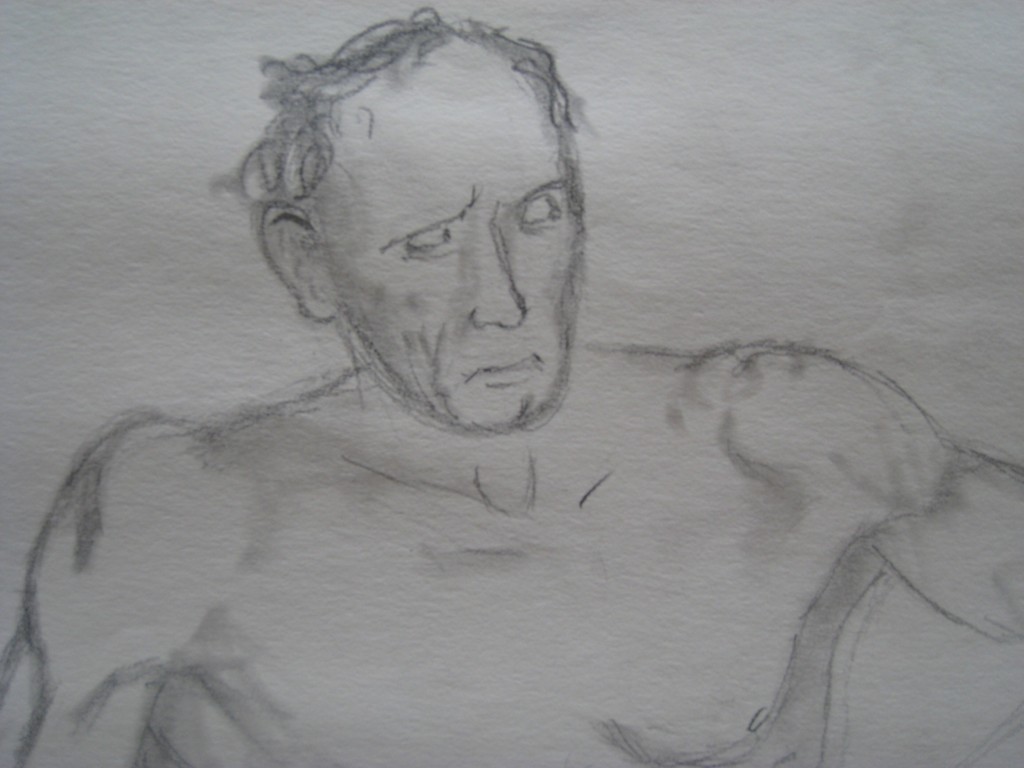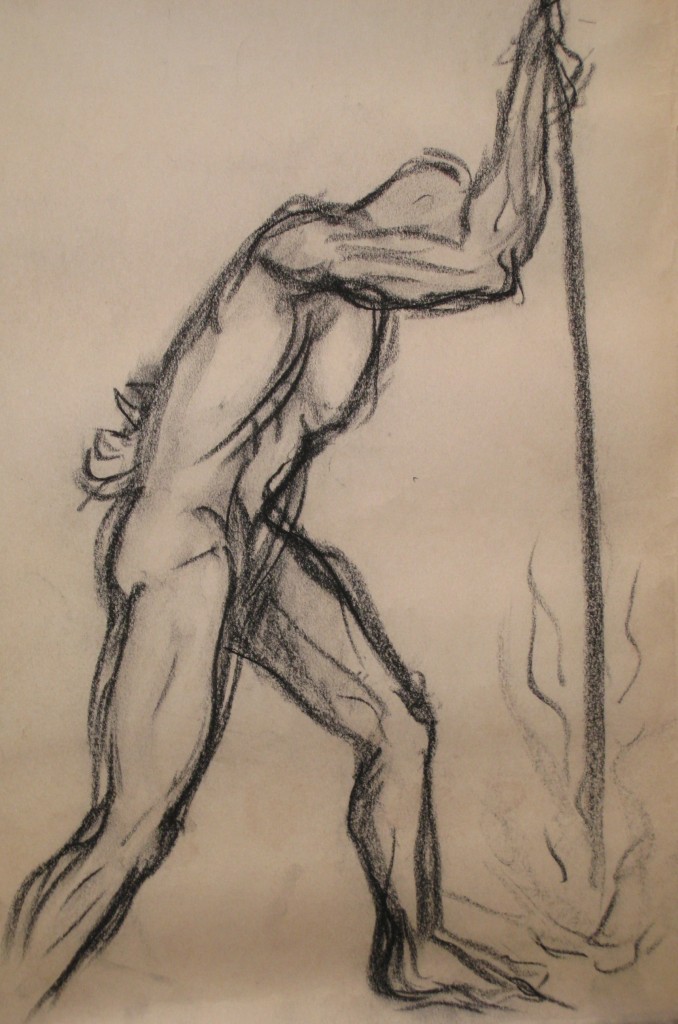“You can’t be serious!” ??
This man is realizing with helpless disgust that he can do nothing to stop this foolishness.
Geoffro – Smoke Detector mix
A project I was on in college at Berklee in 2005 for Geoffro.
I always thought the sounds on this track were so damn good. By the time I got to this mix it was already sounding awesome.
Songs I Can Do…expressed as sets :o
Recently I got out the old guitar, for singin’ with, and went over some old tunes I used to know. As I dusted off the cob webs I found more little jewels I used to own<?>. Anyway, here’s a running list…
Reconsider Baby – Lowell Fulson
Biggest Lie – Elliott Smith
I Figured You Out – Elliott Smith
Beast For Thee – Bonnie Prince Billy
Bed Is For Sleeping – Bonnie Prince Billy
Lost Cause – Beck
Billy Gray – Norman Blake (great name)
Tore Down – Freddie King
Between The Bars – Elliott Smith
Division Day – Elliott Smith
Down Bound Train – Bruce “the boss” Springsteen
(What I’d like to do) ∩ (What I can do) ~ Artistic Direction?
How to prove the quadratic formula, by completing the square
You may be familiar with completing the square. If so, skip down a bit till you see a blue word.
To prove the quadratic equation by completing the square, we must first know how to complete the square.
Consider (x + b)2
Well doesn’t (x + b)2 = (x + b)(x + b)?
…and (x + b)(x + b) = x2 + xb + bx + b2, which equals
= x2 + 2bx + b2
Therefore,
(x + b)2 = x2 + 2bx + b2
The above is an example of a perfect square.
Ok, keep this in mind…
Now then, let’s say you’re given a weird polynomial that doesn’t obviously factor. Like…
2x2 + 10x – 2
This polynomial may very well not be a perfect square, but I can use the fact that I know what form a perfect square takes to solve the problem and find all the x intercepts (roots) of the function.
The first thing I like to do is divide the polynomial by the coefficient of the highest power. The resulting polynomial will have the same roots as the original.
So…
x2 + 5x – 1 is now what we’re working with, but the answers for x will be the same as 2x2 + 10x – 2.
We now have to set the expression equal to zero, in order to find out where the graph intercepts the x axis. Keep in mind that if y = 0 then the graph has to be touching the x axis somewhere, for real roots.
So…
x2 + 5x – 1 = 0
Your options now are to complete the square, or use the quadratic formula if you have it memorized.
Let’s say you don’t have the quadratic formula memorized.
To solve the problem you’ll need to complete the square, and here’s how to do it.
Remember (x + b)2 = x2 + 2bx + b2?
Could we apply that to the problem somehow?
Well, what if we moved the 1 to the other side of the equation such that…
x2 + 5x = 1
Then couldn’t we take the left side of the equation (x2 + 5x), which looks a lot like the first part of x2 + 2bx, and just find the + b2 that goes with x2 + 5x?
If we did that, we’d set 2bx = 5x which would give 5/2. This is our b value, 2.5 or 5/2. Now we just have to square that value to get our + b2.
This gives…
x2 + 5x + (25/4) = 1
…but remember that whatever we add to the left side of the equation we have to add to the right.
So…
x2 + 5x + (25/4) = 1 + (25/4)
Now can we not re-express x2 + 5x + (25/4) as (x + 2.5)2 ?
Since b = 2.5 or 5/2 as we stated earlier, and because (x + b)2 = x2 + 2bx + b2 ?
Answer: yes, we can.
So…
(x + 2.5)2 = 1 + (25/4)
(x + 2.5)2 = (4/4) + (25/4)
(x + 2.5)2 = (29/4)
And…
x + 2.5 = ±(√29)/2
Then simply take the 2.5 over as well…
x = [-5 ±(√29)]/2
And there’s your answer…
x can either equal [-5 + (√29)]/2, or [-5 – (√29)]/2.
word!~
To prove the quadratic formula by completing the square all we have to do is the same process above, on a generalized version of a square polynomial.
So we start with the standard (generalized) form of a square polynomial:
Ax2 + Bx + C
Now the idea is to get from the above to this:
x = [-B ± √(B2 – 4AC)]/2A …algebraically.
Set it equal to zero, to find the roots (x intercepts).
Ax2 + Bx + C = 0
Then just complete the square!
Let’s put c on the right side of the equation.
Ax2 + Bx = -C
Then divide by A, to get the x2 + bx from x2 + bx + b2. Remember that (x + b)2 = x2 + 2bx + b2
x2 + (B/A)x = (-C/A)
Now we have to complete the square of x2 + (B/A)x. Just like before we set 2bx equal to (B/A)x to find b.
2bx = (B/A)x
b = (B/2A)
So…
b2 = (B/2A)2
And…
x2 + (B/A)x + (B/2A)2 = (-C/A) + (B/2A)2
But (x + b)2 = x2 + 2bx + b2, remember?
So…
[x + (B/2A)]2 = (-C/A) + (B/2A)2
or
[x + (B/2A)]2 = (-C/A) + (B2/4A2)
Now, let’s find common denominators for the right side of the equation and simplify.
So…
[x + (B/2A)]2 = (-C/A) + (B2/4A2)
becomes…
[x + (B/2A)]2 = (-4AC + B2)/4A2
take the square root of both sides…
x + (B/2A) = ± √[(-4AC + B2)/4A2]
simplifying the right side…
x + (B/2A) = ± √(B2 – 4AC)/2A
moving the (B/2A) term to the right side, just like in the former problem…
x = (-B/2A) ± √(B2 – 4AC)/2A
when we combine the denominators to simplify, we get…here it is…
x = [-B ± √(B2 – 4AC)]/2A
Artist showcase: Melissa Lange
It seems like Melissa is in the middle of defining a new style for herself. I love it.
Melissa Lange is an Austin, TX based artist.